Background
In North America, we have a standardized way of producing braille number lines for grades 4 and upward in standardized tests and math textbooks. See 6.5.1 Number Lines in Guidelines and Standards for Tactile Graphics, 2022 at: https://www.brailleauthority.org/guidelines-and-standards-tactile-graphics. Also, all number lines transcribed in Nemeth within UEB contexts must be enclosed within Nemeth Code switch indicators even though numbers may not be modified. Nemeth braille number lines are created on the computer using any six-key entry software program and specific Nemeth code mathematical number line designations, which are explained in a transcriber’s note. The student can easily produce these as well, using a braille writer. These tactile number lines are also quite “visual” and therefore rather easy for a sighted math teacher to interpret, given the rules for symbols.
The following symbols are used to create number lines:
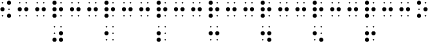
![]() (dots 2,4,6) left-pointing arrowhead
(dots 2,4,6) left-pointing arrowhead
![]() (dots 2,5) line (axis line)
(dots 2,5) line (axis line)
![]() (dots 1,2,3,5) coordinate scale mark
(dots 1,2,3,5) coordinate scale mark
![]() (dots 1,3,5) right-pointing arrowhead
(dots 1,3,5) right-pointing arrowhead
Appropriate Nemeth code numbers (without numeric indicators)
The next symbols are used to create the graph on the number line.
![]() (dots 1,2,3,4,5,6) solid (filled-in) circle (point included) placed above the number line
(dots 1,2,3,4,5,6) solid (filled-in) circle (point included) placed above the number line
![]() (dots 1,3,4,6) open circle (point not included) placed above the number line (only necessary when graphing an inequality involving “<” or “>” or “not equal to”)
(dots 1,3,4,6) open circle (point not included) placed above the number line (only necessary when graphing an inequality involving “<” or “>” or “not equal to”)
![]() (dots 2,3,5,6) shading of the rest of the points included in the solution on the number line itself
(dots 2,3,5,6) shading of the rest of the points included in the solution on the number line itself
General Instructions
When graphing an inequality on a number line, first space down a line.
Then, create the number line: left arrow, line, line, scale mark, line, line, scale mark, … right arrow (add more or less “line” depending on the problem and preciseness required). Some of us prefer to say “left arrow; 2,5; 2,5; r; 2,5; 2,5; r; … right arrow.”
Next, place the proper coordinate (for the preciseness required) under each scale mark. (We leave off numeric indicators to allow better spacing or you can label every other scale mark, or every fifth one – whatever is appropriate for the specific graph.)
Above the number line, indicate whether your solution will include an open and/or closed circle at the appropriate coordinate.
“Shade” on the number line all of the points that represent the solution, in addition to the boundary point(s) designated with open and/or closed circles. To designate that the shading continues infinitely to the left or right, use an additional appropriate arrowhead.
It is so much easier to just do this than describe it. The students get in a rhythm, and they do it very quickly. I created a series of number lines on the computer and gave my students a worksheet similar to the ones in print, and most of them rejected it. They preferred doing the number lines themselves and changing the scale marks and numbered coordinates to fit each particular problem. It is perfectly all right for blind students to be more proficient at graphing than their sighted peers.
Detailed Example
Solve and graph 2x-5 < 1 on a number line.
The student would first solve the inequality and get x < 3.
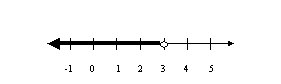
They would then construct a number line and space it such that they could have at least a couple of coordinates larger than 3 and a few smaller than 3; perhaps label it from -1 through 5, and add an additional left pointing arrowhead. Then they would braille an open circle above the scale mark at coordinate 3. Finally, starting just to the right of the 2nd left-pointing arrow, they would “shade” the number line all the way up to (but not include) the 3.
Students may find it easier to shade on top of scale marks, but transcribers do not in the graphs below.


More Examples
Graph the following integers on a number line: -2, -1, 0, 1, 2.
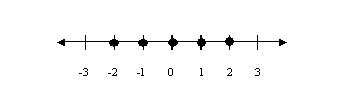

Graph x ≥ -2.


Graph 2 < x ≤ 1.


See Number Lines in the Nemeth Focused Lessons of the Nemeth Braille Code Curriculum for more practice and activities.
This article was originally published in 2003 in Division on Visual Impairments Quarterly, 48(2), 9-11. Updated in 2024.




